En las últimas décadas han surgido una gran variedad de modelos computacionales basados en agentes para estudiar fenómenos de distinta naturaleza (ver sección 4.1). En este camino se han plateado modelos que son paradigmáticos y que sentaron la base para proponer modelos más sofisticados. En esta sección se mostrarán cuatro modelos representativos, se analizarán sus dinámicas, se mostrará el simulador computacional, y se dejarán algunas preguntas abiertas para que nuestros lectores, las analicen y puedan adentrarse a la MBA.
En los años setenta, John H. Conway, matemático británico, propuso uno de los autómatas celulares más estudiados, LIFE o también conocido como el Juego de la Vida. Este modelo fue popularizado por primera vez por Martin Gardner (1970) en su columna de juegos matemáticos de la revista Scientific American. El modelo se desarrolla en una retícula donde se ejecutan un conjunto de reglas muy simples que consisten en actualizar el estado de cada una de las celdas a partir de la información de las celdas vecinas. Estas reglas de carácter local generan una gran diversidad de comportamientos de manera global, en otras palabras, reglas simples generan un comportamiento complejo.
Los autómatas celulares son sistemas dinámicos discretos compuestos de manera espacial por un conjunto de celdas homogéneas ordenadas en forma retícula y una parte temporal definida por ciertas reglas de aplicación (ver Tabla 2). LIFE o el Juego de la Vida es un autómata celular bidimensional con dos posibles estados, 0 y 1, a menudo se describen como celdas prendidas o vivas (uno) y celdas apagadas o muertas (cero); el tiempo de evolución es discreto, t=0, 1, ..., k. La actualización del estado de la celda está regida por los valores de sus ocho celdas adyacentes a través de una vecindad de Moore (ver Figura 2). Las reglas locales de evolución son las siguientes:
1. Si la celda está apagada o muerta y tiene exactamente 3 vecinos vivos alrededor, la celda nace.
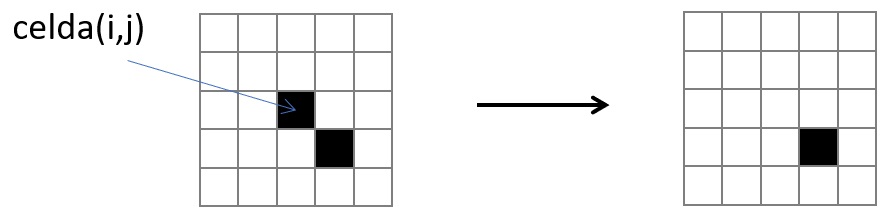
2. Si la celda viva tiene un solo vecino muere por aislamiento.
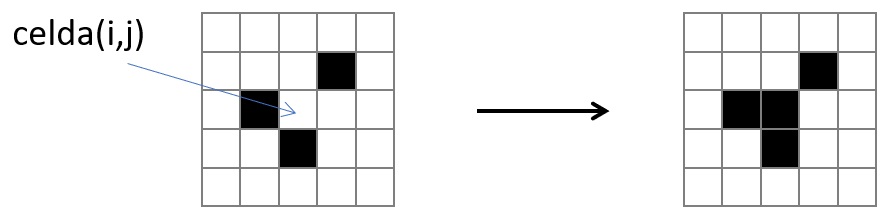
3. Si la celda tiene más de tres vecinos muere por sobrepoblación.
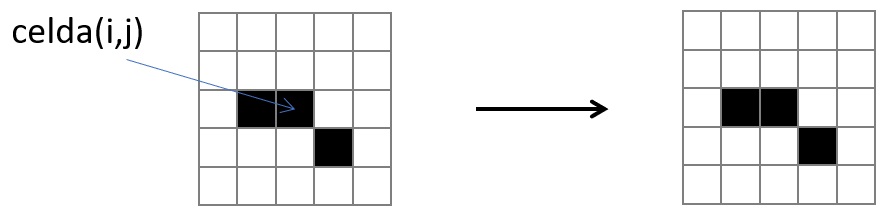
4. Si la celda tiene 2 o 3 vecinos vivos a su alrededor la celda se mantiene viva
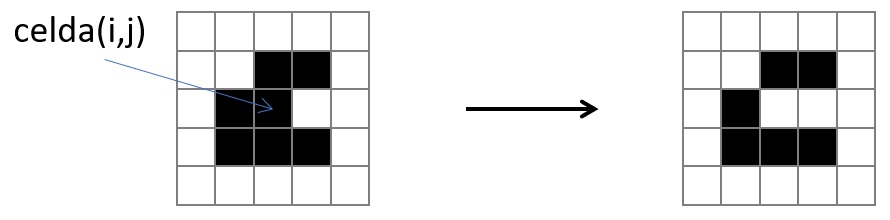
Estas reglas se aplican a cada una de las celdas en la retícula, cuando todas han sido actualizadas, entonces se cumple el primer tiempo de evolución. De esta manera, se puede simular la evolución y observar los cambios que se generan en el sistema.
Figura 6: El entorno se constituye por una retícula homogénea de n x n celdas, por ejemplo, n = 100. En (A) se muestra una condición inicial aleatoria al tiempo t=0, y en (B) la evolución del sistema en el tiempo t = 100.
Aun cuando, se inicia con condiciones iniciales aleatorias, es decir, sin ninguna estructura, surgen patrones con diferente comportamiento, por ejemplo, se identifican estructuras estables, es decir, no hay cambio a través del tiempo; periódicas, se repiten cada cierto tiempo; inestables, cambian y no persisten en el tiempo; y periódicas pero que se trasladan en el espacio, estos son conocidos como planeadores o gliders.
En la Figura 7, se presentan algunas estructuras con ciertas propiedades, de (A) a (D) son ejemplos de estructuras estables, es decir, que no cambian en el tiempo y surgen comúnmente en cualquier evolución de LIFE con condiciones iniciales aleatorias, a (A) se el conoce como “bloque”, (B) como “piscina”, (C) como “nave”, y (D) como “bote”. Las estructuras mostradas en (E) y (F) son estructuras periódicas u osciladores, es decir, cada cierto tiempo repiten sus estados; se le conoce como “blinker” y “hongo” respectivamente y conmutan entre dos estados. Las estructuras más interesantes son las que se desplazan por el espacio como el “glider” o planeador (G), el cual tiene cuatro estados distintos desplazándose sobre el espacio; a (H) se le conoce como “nave ligera” y puede trasladarse de manera horizontal, en este caso, de derecha a izquierda.
Figura 7. Estructuras con comportamientos interesantes en LIFE.
La gran variedad de estructuras que se pueden descubrir en LIFE es inmensa, ¿se podrá diseñar algún patrón con propiedades específicas? Como ejemplo, existe un patrón llamado “pistola de gliders”, el cual es un generador de gliders, cada cuatro tiempo genera una estructura de este tipo, la aportación es el control que se tiene sobre estos pulsos, lo cual permite la construcción de estructuras más complejas, como circuitos lógicos.
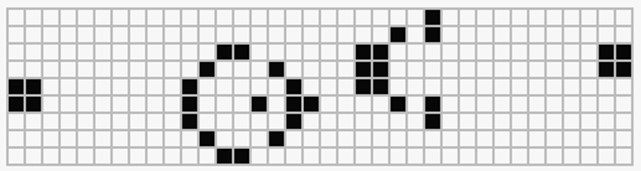
Figura 8. Pistola de gliders.
Se invita al lector a replicar la condición inicial de la Figura 8, para observar la propagación de gliders, para este propósito puede usar el simulador de LIFE (Wilensky,1998) que está incluido en la biblioteca de modelos de NetLogo, a través del siguiente link: http://www.netlogoweb.org/launch#http://ccl.northwestern.edu/netlogo/models/models/Sample%20Models/Computer%20Science/Cellular%20Automata/Life.nlogo.
En este apartado se utilizará el simulador de LIFE desarrollado en el proyecto PAPIME No. PE310320 en el año 2020 como parte del Taller Sistemas complejos aplicados al a Economía y Fenómenos Sociales. A través del siguiente link: https://complejidad-iiec.web.app/cursotaller2020/mba/modelos/juego/index.html, se le invita al lector a ejecutar el modelo del juego de la vida, observar su evolución y los patrones que surgen con diferentes condiciones iniciales.
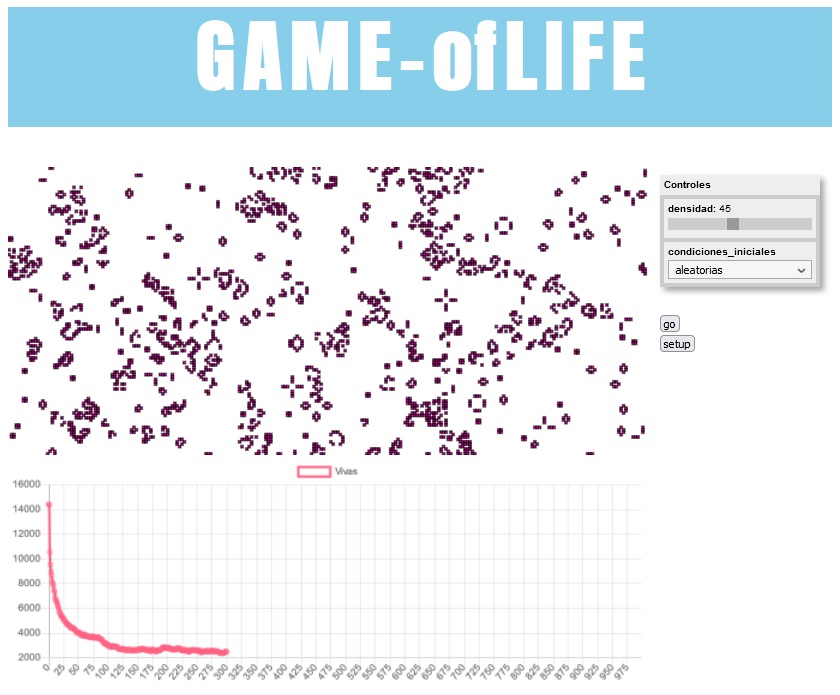
Figura 9. Simulador de LIFE.
La interfaz (ver Figura 9) está constituida por una ventana de visualización, conocida como entorno o mundo, donde se muestra la evolución del sistema a través del tiempo. El botón “setup” se utiliza para iniciar o reiniciar el modelo, actualiza el estado inicial del sistema para comenzar la simulación, y el botón “go” ejecuta la simulación. El seleccionador “condiciones_iniciales" tiene preestablecidos varios patrones que generan dinámicas interesantes. Por otro lado, el cambio de las celdas vivas a través del tiempo se puede seguir con la gráfica "Vivas".
Usualmente, como primer acercamiento para estudiar un sistema dinámico, se inicializa el sistema con condiciones iniciales aleatorias. En LIFE, se han experimentado a lo largo de los años para encontrar comportamientos interesantes, con un poco de práctica se pueden llegar a construir escenarios realmente sorprendes con el fin de realizar una tarea objetivo, por ejemplo, estructuras periódicas que se trasladan sobre el espacio, generadores de letras, incluso computar LIFE con el mismo LIFE (Zucconi, 2020).
A través de la ventana o el mundo de agentes se puede dar seguimiento a la dinámica, ¿cómo evoluciona?, ¿qué tipo de patrones surgen? Con ayuda de la gráfica incluida en la interfaz del simulador, se mide de manera global como cambia el número de celdas vivas a través del tiempo. Unas preguntas para el lector son las siguientes: en una retícula de 100 x 100 celdas, ¿cuántas posibles condiciones iniciales distintas podemos definir?, ¿podríamos explorarlas todas.
El Juego de la Vida de John Conway es un buen ejemplo para analizar la diversidad de estructura que surgen en su evolución, por tal motivo, se convirtió en un icono de los modelos y simulaciones computacionales basados en autómatas celulares. A partir de reglas sencillas se genera comportamiento complejo. El modelo tiene propiedades de cómputo universal (Durand, 1988), es decir, que en teoría se puede implementar cualquier proceso algorítmico instanciando el modelo con una entrada adecuada.
Uno de los modelos basados en agentes más sencillos, es la hormiga de Langton (). La hormiga es un agente autónomo que interactúa con su ambiente pero que actúa de forma independiente, no es controlado por algún líder y no sigue ningún plan global. Son dos reglas muy sencillas:
En la Figura 10, se representan las primeras iteraciones del modelo. En (A) se muestra la condición inicial, una hormiga orientada hacia el este sobre un entorno compuesto de celdas blancas; en (B) se ejecuta la regla 1, ya que se encuentra parada sobre una celda blanca; de (C) a (E) ejecuta nuevamente la regla 1; en (F) la situación cambia ya la hormiga esta parada sobre una celda negra (que en momentos previos ella misma modifico), así que se ejecuta la regla 2, así que pinta la celda de blanco, rota a la izquierda y avanza; en (G) y (H) nuevamente aplica la regla 1. Básicamente, la hormiga interactúa con el entorno, y en función de la información recibida rota sobre su eje, modifica el entorno y avanza.
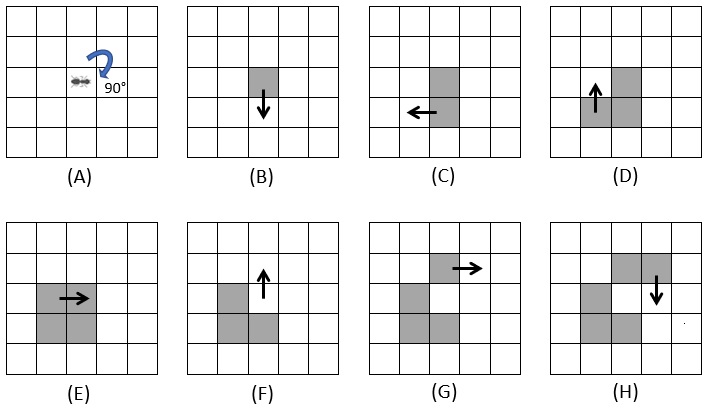
Figura 10. Primeras iteraciones del modelo del a hormiga de Langton.
Esta dinámica es muy simple, ¿podría generar algún comportamiento interesante? Se invita al lector a que ejecute el modelo implementado en NetLogo en el siguiente link: http://www.complejidad.iiec.unam.mx/libro/capitulo4/GICE_HormigaDeLangton2022.html.
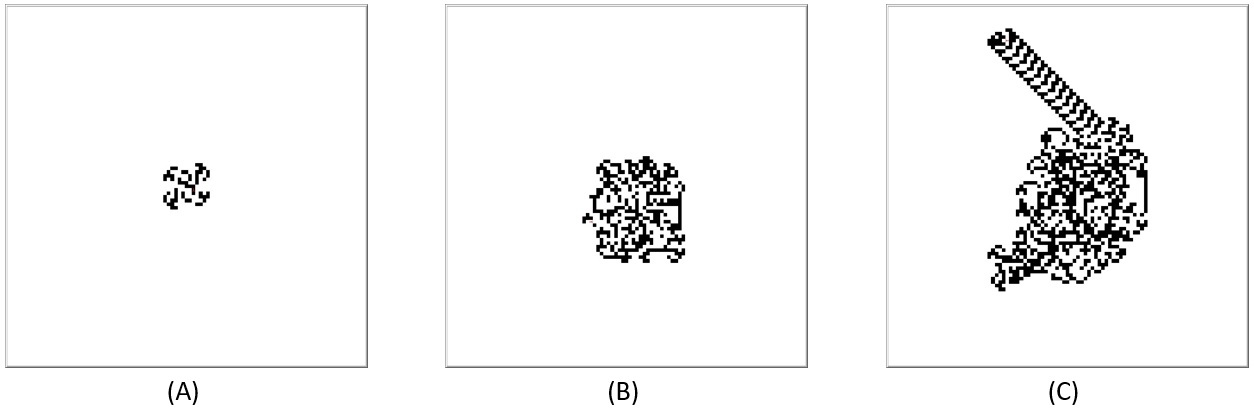
Figura 11. Evolución del modelo de la hormiga de Langton. Se muestran diferentes estados del entorno al tiempo t = 477 (A), t=4500 (B) y t= 11350 (C).
En la Figura 11, se muestran estados representativos de la evolución del sistema. En (A) se muestra el estado del sistema en el tiempo 477, en el cual, la hormiga genera una estructura regular; en (B), t =4500 y el conjunto de celdas no tiene algún patrón discernible, es más como una estructura aleatoria; y en (C), alrededor de t=11350, ocurre algo espontáneo, la hormiga inicia la construcción de una estructura periódica que se propaga al infinito, es llamada “carretera”.
Esta carretera no está definida en la programación de las dos sencillas reglas de la hormiga, entonces ¿de dónde surge? ¿qué condición se tiene que satisfacer para que surja la carretera? Esta estructura es considerada como una propiedad emergente del sistema, ya que es nueva información que surge en una escala global, además, es el resultado de la interacción entre la hormiga y su entorno. Las posiciones de las celdas negras y blancas juegan un papel relevante, en el trabajo de Gajardo y colaboradores (2002), se propone una condición inicial para que la hormiga inicie de manera casi inmediata la construcción de la carretera (ver Figura 12). Esto puede generar algunas preguntas, por ejemplo, dada cualquier condición inicial del entorno ¿la hormiga podrá construir la carretera?, ¿cómo lo mostramos? Se invita al lector, a que pruebe distintas condiciones iniciales en el simulador de la hormiga de Langton.
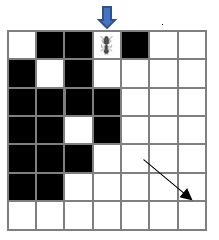
Figura 12. Condición inicial para generar la carretera. La hormiga entra por la parte superior en dirección norte, y se genera una carretera en dirección sureste.
Este modelo con un agente e interacción con el entorno nace en el área de la vida artificial, donde se desarrollan modelos con elementos inspirado en los fenómenos reales, y cuya motivación responde a preguntas como ¿qué pasaría si …?
Estos modelos artificiales, LIFE y la hormiga de Langton, hacen reflexionar sobre la complejidad de los sistemas, aun cuando, las reglas de interacción son sencillas, las propiedades que surgen no lo son, no hay una relación lineal entre el desempeño del agente y el resultado global del sistema.
Es importante notar que, en los sistemas socioeconómicos, como se planteó en el capítulo 2, los agentes (personas) actúan por medio de reglas sencillas, pero es en la interacción con el medio y otros agentes, cuando surge la complejidad.
El economista Thomas Schelling, premio nobel de Economía en 2005 por sus aportaciones en el entendimiento de la cooperación y el conflicto, propuso un modelo para estudiar la segregación de grupos a través las decisiones individuales fomentadas por la preferencia de vivir en una región con personas del mismo grupo. En sus resultados mostró que dos grupos de personas pueden cambiar el entorno a un patrón altamente segregado sin una organización preestablecida.
El trabajo original de segregación de Schelling (1971) es relevante en el contexto de la modelación basada en agentes, ya que es un trabajo pionero en el área y ha contribuido al desarrollo de esta línea de investigación. Cuando Schelling planteó este trabajo, no estaba establecida la MBA, incluso se estaban conformando trabajos en el área de autómatas celulares. En su trabajo, Schelling llamó a este sistema de tipo tablero de ajedrez o checkerboard con la actualización de estados a través de vecindades (elemento principal en la MBA), además se puede destacar que, sin la ayuda de computadoras, realizó análisis en retículas de 13x16 celdas y mostró el surgimiento de patrones globales segregados. Una implementación de este modelo se puede encontrar en la biblioteca de NetLogo (Wilensky, 1977).
El modelo basado en agentes de segregación de Schelling es un modelo residencial, el cual parte de las siguientes premisas:
Esta dinámica es descentralizada, ya que no hay un agente líder que imponga ciertas conductas o que guíe el proceso. Las decisiones individuales, generan nuevas propiedades en el sistema en una escala global, llevando al sistema a exhibir patrones de segregación.
Se invita al lector a ejecutar el modelo de segregación de Schelling a través del siguiente enlace:https://complejidad-iiec.web.app/cursotaller2020/mba/modelos/Segregation/index.html . La Figura 13, muestra la interfaz del simulador y los elementos gráficos para realizar los análisis.
Figura 13: Partes básicas de la interfaz del modelo implementado en la plataforma NetLogo.
En el modelo, los agentes consideran una vecindad de Moore para tomar una decisión en función del parámetro %-similitud-requerida. Las reglas son las siguientes:
El modelo consta de la ventana del entorno donde se puede ver las posiciones de los agentes según su color y los lugares vacíos. También de manera general se observa la formación de patrones o estructuras colectivas.
El botón "setup" se utiliza para iniciar o reiniciar el modelo, actualiza el estado inicial del sistema para comenzar la simulación, y el botón "go" ejecuta la simulación.
Los deslizadores cambian los valores de los parámetros globales.
La gráfica porcentaje de similitud muestra el promedio del porcentaje de vecinos del mismo grupo para cada agente; y la gráfica porcentaje de no felices mide el promedio de los agentes que no encuentran una posición satisfactoria.
Al presionar "setup" se inicializan las posiciones de los agentes de ambos grupos de manera aleatoria, es decir, no se observa patrón alguno. Cuando se ejecuta el botón "go" los agentes empiezan a evaluar su entorno (local) y tomar la decisión de moverse a otro lado o permanecer en su sitio. Esta evaluación cambia debido al entorno, en un momento pueden estar "satisfechos" pero en otros momentos no estarlo.
Figura 14. Distribución aleatoria de los agentes en el espacio en el tiempo cero.
Al ejecutar el modelo se puede observar en la ventana de agentes, como las decisiones individuales afecta el entorno y hay cambios de posición. Para medir de manera global como satisfacen sus requerimientos (estar con los de su mismo grupo) se crean indicadores globales, mostrados en las gráficas de la Figura 15.
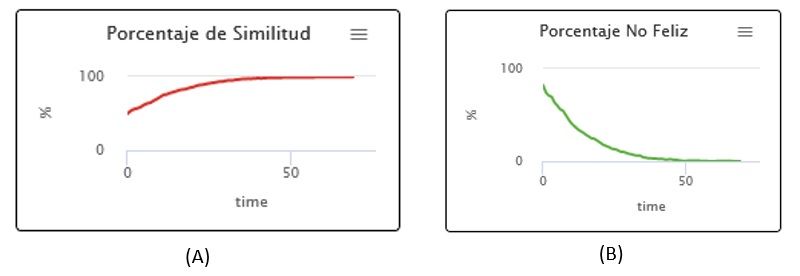
Figura 15. (A) Porcentaje de similitud. Es una medida global del sistema que indica la formación de grupos en el entorno. (B). Porcentaje no felices. Este indicador muestra el número de personas que no encuentran una posición satisfactoria en el entorno.
Los tres parámetros del modelo juegan un papel muy importante, con la variación de parámetros se puede cambiar de una dinámica a otra, es decir, en el contexto del modelo, de patrones poco segregados, a muy segregados, y a no tener ningún tipo de patrón. El parámetro principal es el porcentaje de similitud requerida "%-similitud-requerida", ¿cómo cambia el sistema con diferentes valores del parámetro?
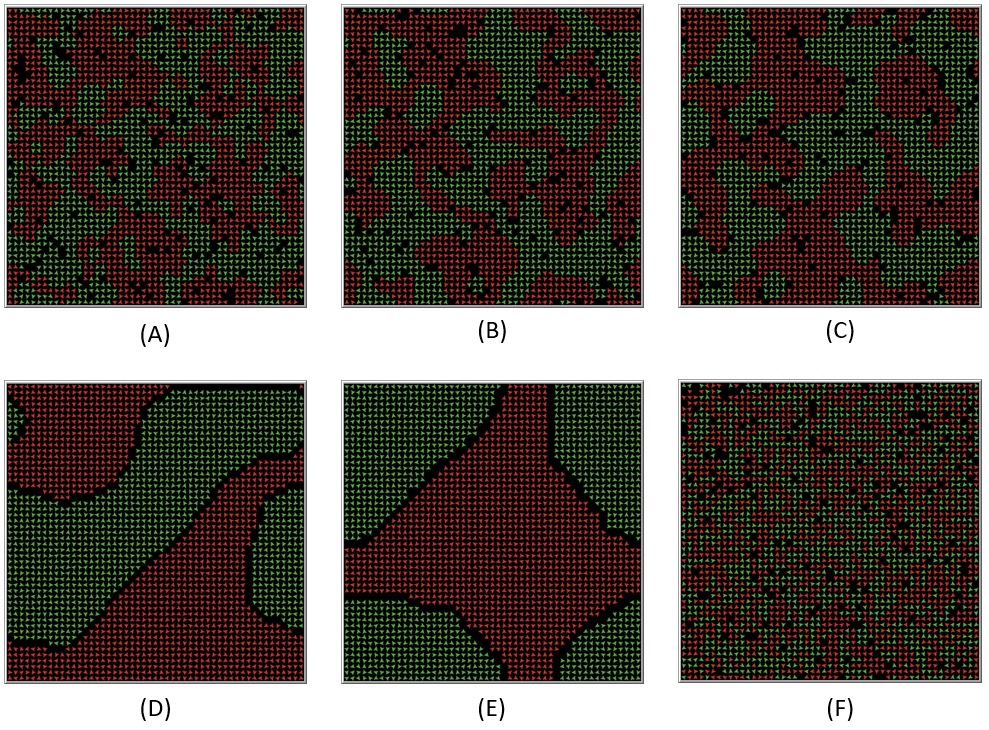
Figura 16. Resultado de las simulaciones con la variación del parámetro %-similitud-requerida con los valores, 30, 40, 50, 60, 70 y 80 respectivamente.
A partir de la Figura 16, ¿qué diferencia en las dinámicas observas? A partir de las restricciones impuestas por los mismos agentes, los patrones de segregación cambian, o incluso pueden llegar a otro régimen dinámico donde las condiciones del entorno son tan restrictivas que no hay ninguna forma de satisfacerlo, a esto se le conoce como sistema frustrado, como se muestra en la Figura 16(F).
El modelo de segregación de Schelling permite entender como a través de decisiones individuales de los agentes (descentralización) se pueden formar grupos segregados solo con la preferencia de vivir con un cierto porcentaje del grupo al que pertenece. Estas decisiones locales generan un patrón global descrito por la formación de cúmulos en mayor o menor grado.
El problema trata de la estimación del número de asistentes a un bar realizado por un grupo de personas (agentes), los cuales, tiene que decidir si asisten o no a dicho bar, el lugar es disfrutable si no se encuentra saturado de personas. La parte central es la toma de decisión de cada agente utilizando el razonamiento inductivo en un entorno cambiante. El agente tiene una memoria y un cierto número de estrategias para tomar su decisión, además, no hay comunicación entre agentes, bajo este esquema, ¿los agentes podrán llegar a predecir la cantidad de asistencia al bar? El problema del Bar el Farol fue planteado inicialmente por el economista de origen irlandés Brian Arthur (1994). Se trata de la estimación de determinado predictor de asistencia a un bar de un grupo de agentes en donde, cada agente, tiene que decidir la asistencia o no a dicho bar. Lo que propone Arthur es modelar la toma de decisión de los agentes con un modelo interno determinista (reglas de interacción) para asistir a un bar utilizando el razonamiento inductivo en un entorno cambiante. Específicamente plantea el siguiente problema: en Santa Fe, Nuevo México, existe un Bar llamado El Farol, en donde los jueves por la noche hay música irlandesa en vivo, y hay un número finito de personas que desean ir al bar, el problema es que es un bar modesto y no es agradable ir si está repleto. Cada individuo tiene que decidir en forma independiente si asiste o no.
Conforme a los preceptos de la ciencia experimental, el razonamiento inductivo es un proceso que parte de casos particulares que, tras la observación, uno tras otro caso, a través de la experiencia determina una conclusión más general. Arthur lo aplica al caso de la modelización de la toma de decisión de agentes individuales heterogéneos con racionalidad limitada. En el problema del Bar El Farol, el aporte de nuestro autor es dejar evidencia analítica y empírica de una toma de decisión más realista y, al mismo tiempo, poner en entredicho la toma de decisión de agentes homogéneos con racionalidad completa de la teoría neoclásica.
Las hipótesis del modelo son las siguientes:
Se tienen las siguientes "reglas" de comportamiento para los agentes:
El problema es que, todo el mundo interesado en asistir al bar tiene que decidir al mismo tiempo; por ejemplo, suponga que la venta de boletos para entrar al bar es los jueves a las 12:00 horas y no es posible esperar para ver cuánta gente antes que ellos han decidido ir al bar. ¿Cómo será la dinámica bajo estos supuestos?
Se invita al lector a ejecutar el modelo del Bar “El Farol” a través del siguiente enlace: https://complejidad-iiec.web.app/cursotaller2020/mba/modelos/pagina-farol/index.html . La Figura 17, muestra la interfaz del simulador y los elementos gráficos para realizar los análisis.
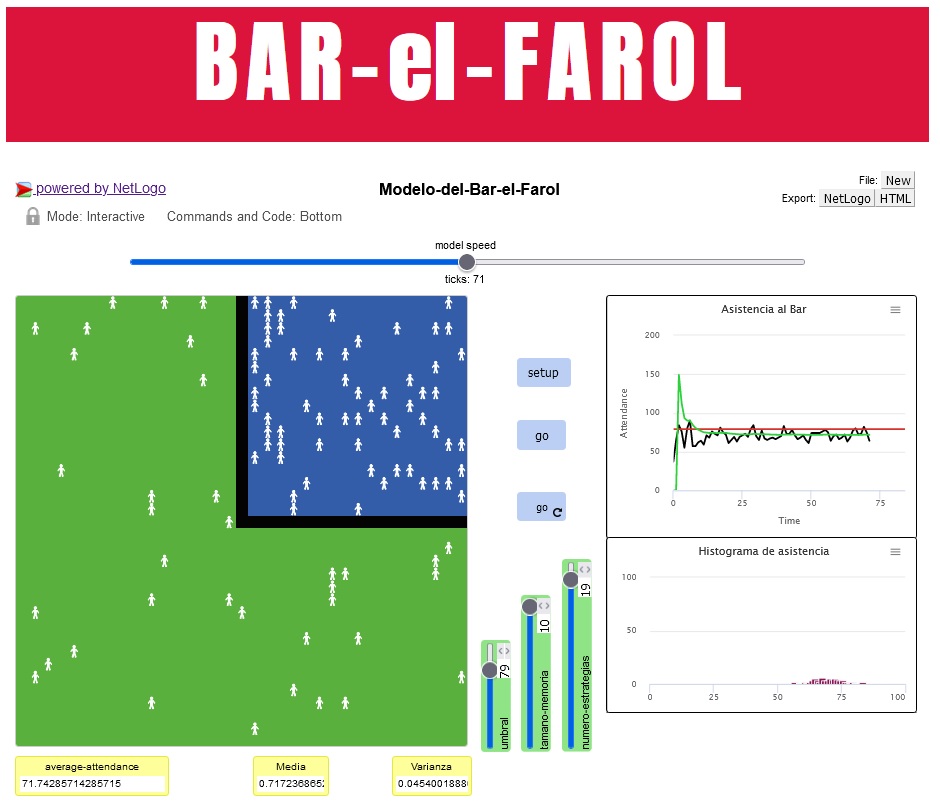
Figura 17. Elementos del simulador del Bar “El Farol”.
Al ejecutar el modelo computacional encontramos la ventana del espacio de agentes, la parte más atractiva del simulador ya que en ella se muestra cómo evoluciona el modelo (ver Figura 17).
Las partes principales de la interfaz son:
Mientras que los parámetros del modelo:
El botón "setup" se utiliza para iniciar o reiniciar el modelo, actualiza el estado inicial del sistema para comenzar la simulación, y el botón "go" ejecuta la simulación. Los datos de salida o los resultados simulados se pueden seguir con la gráfica "Bar attendace". Los deslizadores permiten establecer los rangos de valores para los parámetros. Al modificar los valores de entrada de la simulación se crean sistemas con características y propiedades distintas.
En la interfaz, la asistencia semanal se representa mediante una serie de tiempo se actualiza continuamente, y el desplazamiento de los individuos hacia el Bar cada semana se puede visualizar en la ventana del entorno del modelo (ver Figura 17).
El modelo considera: 1) un conjunto de tres parámetros que se pueden variar en cada simulación: memory-size, number-strategies y overcrowding-threshold; 2) asigna a cada uno de los individuos de la población un conjunto de estrategias potenciales a utilizar en la predicción de la futura ocupación del bar; y 3) determina un criterio para que cada individuo elija la “mejor” estrategia entre las que tiene asignadas en cada una de las semanas para realizar la próxima predicción de ocupación.
Se pueden realizar distintas simulaciones ejecutando el simulador con diferentes valores para el tamaño de la memoria histórica y el número de estrategias que puede gestionar un individuo. La observación de los resultados de la simulación, con su posterior análisis, permiten estudiar la evolución del sistema. Por ejemplo, ¿qué pasa con la variabilidad de la asistencia u ocupación del bar a medida que fijamos el tamaño de memoria y variamos el número de estrategias posibles que un individuo puede manipular?
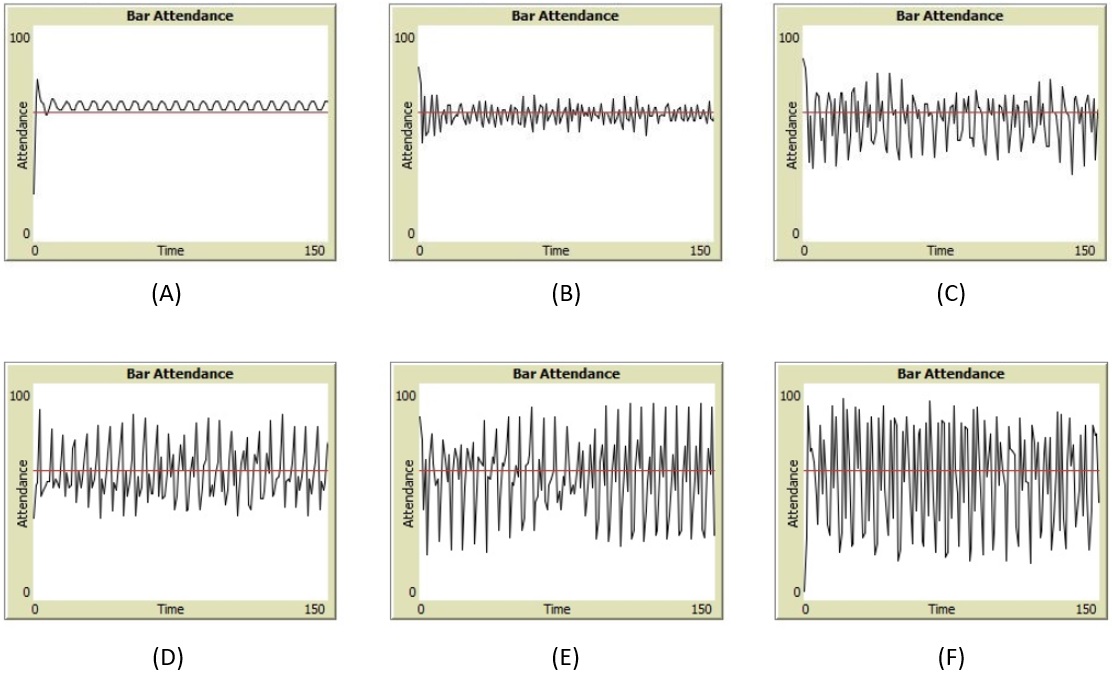
Figura 18. Resultados de las simulaciones con valores fijos para los parámetros overcrowding-threshold= 60 y memory-size = 5, con valores diferentes para el parámetro number-strategies: 2, 5, 8, 11, 14 y 20 respectivamente.
Ahora, ¿qué sucede con la variabilidad de asistencia al bar si mantenemos fijo el número de estrategias y variamos el tamaño de la memoria?
Figura 19. Resultados de las simulaciones con valores fijos para los parámetros overcrowding-threshold = 60 y number-strategies = 10, con valores diferentes para el parámetro memory-size: 2, 4, 6, 8, 9 y 10 respectivamente.
Para completar los escenarios, ¿qué pasa si varía el umbral de hacinamiento y mantenemos fijo el tamaño de la memoria y el número de estrategias?
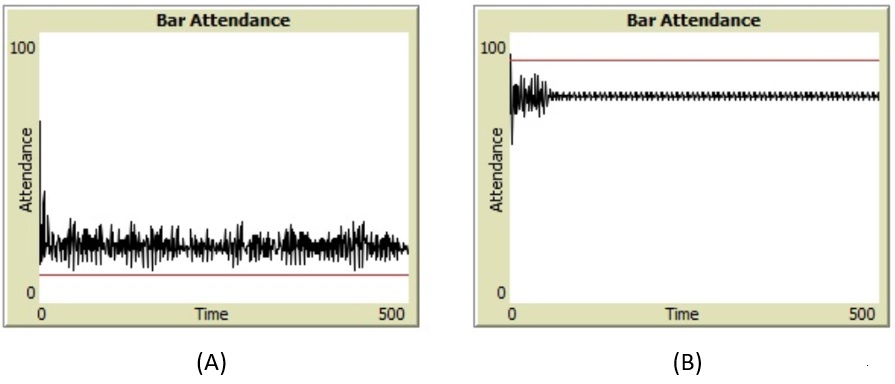
Figura 20. Resultados de las simulaciones con distintos umbrales de hacinamiento y con valores de parámetros fijos memory-size =5, number-strategies =10; (A) overcrowding-threshold=10; y (B) overcrowding-threshold = 90.
Lo que hizo Arthur (1994) para resolver el problema de expectativas del Bar El Farol, dio a los agentes un cierto número de predictores, diferentes entre los agentes, formados con base en las combinaciones del historial de asistencia semanal al bar. La idea que subyace detrás de estos predictores es que, al enfrentarnos a situaciones complejas, tendemos a buscar patrones que se hayan encontrado con anterioridad, y así, en el modelo del bar “El Farol”, los agentes encontrarán este patrón en la información proveniente de un cierto número de semanas. Cada agente utiliza un número limitado de estos predictores, y toma decisiones basándose en el que mejor le ha funcionado, actualizando el ranking de sus predictores tras cada suceso. Los mejores predictores determinan el número de agentes que asisten, y éste a su vez, retroalimenta a los mejores predictores.
La asistencia media converge a 60. De hecho, los predictores se autoorganizan en un patrón de equilibrio o "ecología" en la que los predictores activos, en promedio el 40% pronostica por encima de 60 y no van al bar, y el 60% pronostica por debajo de 60 y van al bar. Esta ecología emergente es de naturaleza casi orgánica. Estos resultados aparecen a lo largo de los experimentos y son robustos a los cambios en los tipos de predictores creados y en los números asignados.
La riqueza del modelo es la dinámica en la toma de decisiones de los agentes que contrasta enormemente con la toma de decisiones en condiciones de racionalidad completa, en un contexto del bar el farol, tenemos los siguientes casos extremos: 1) si el bar no está repleto entonces todo el mundo acudirá, por lo que el bar se saturará, análogamente, 2) si el bar está repleto, entonces nadie acudirá y, por lo tanto, el bar estará vacío.